CMSI 2210: Welcome to Week 06
This Week's Agenda
For this week, here's the plan, Fran…
- Announcements
- Basic Logic Combinations ~ FlipFlops and Adders
- Stanley/Penguin — A Simple CPU
- Parts
- Operation
- Illustrating What Happens Inside
- Fetching and Decoding
- Executing the Instruction
- Writing Programs
- Machine Language
- CISC and RISC
- Wednesday/Thursday: In-class Exercise:
Basic Logic Combinations
The logic gates we investigated last week are much more useful when they are put together in combinations that perform higher level functions. One of the most useful examples is the adder.
Addition
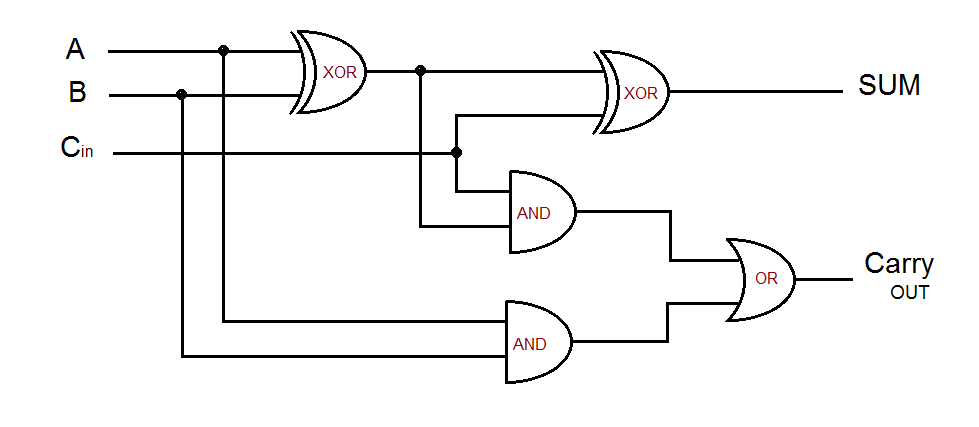
A full-adder circuit is essentially the same as the half-adder we looked at last week. However, in order to support being able to cascade the adders to be of use in addition operations of more than one bit, the full-adder has extra logic to handle a carry input.
Since we now know that an XOR gate will handle single-bit addition, we can cascade two XOR gates to do the addition of two bits with a carry. The A and B inputs go to the first XOR gate, with its output going to one of the second XOR gate's inputs. The C [carry] input goes to the second XOR gate's other input. The truth table for this is shown below.
TWO XOR GATETRUTH TABLE | ||||
|---|---|---|---|---|
| A | B | XORab | Cin | SUM |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
The full-adder carry OUT operation is a bit more complex, but still pretty easy. We need two AND gates and an OR gate in addition to the two XOR gates. The diagram is shown below, with the truth table next to it. In the picture, call the top AND gate A1 and the bottom AND gate A2. The OR gate will just be OR.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
As you can see, the output of the two XOR gates will be exactly the result of binary addition of three one-bit values, the two inputs plus the carry. If there is no carry in, the output is simply the result of adding A and B. If there IS a carry in, it is added to the sum by the second XOR gate. The carry out operation is handled by tapping off of the first XOR gate output, and by also using the carry input. Take some time to walk yourself through the diagram using the truth table so you can convince yourself of the operation. This is a key component in the operation of the CPU! The ability to have carry inputs as well as carry outputs is what allows the CPU to perform mathematical operations on multiple bits at the same time.
Bit State Storage
Next, we need to know how bit values can be stored. When we insert a value into memory [any kind of memory
but in this case register memory] we need to be sure that value will stay put
so it is
available when we need it again. It would be pretty silly to put a 32-bit value into a register and
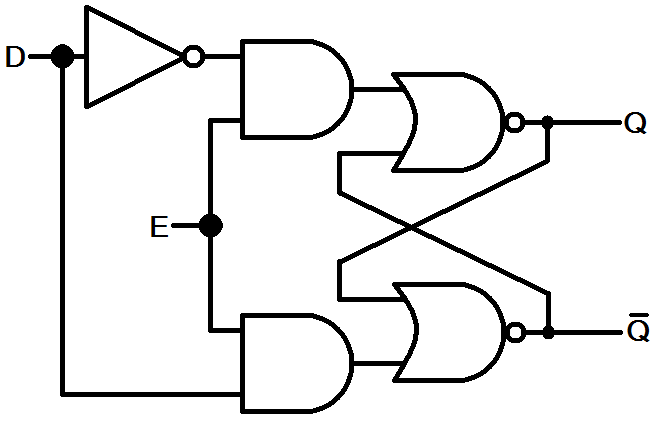
then have the next clock cycle erase it! The logic function that performs such a task is based on the
circuit called a flip-flop. It's gate diagram is shown below.
|
| ||||||||||||||||||||||||||||
As shown, the D latch flop-flop has two inputs – the Data [D] input and the Enable [E] input. As long as the enable input is 1, the Q output will be whatever state D is in. We say Q follows D. If enable goes low, Q will retain its current value regardless of what the data input does. In this way, we can actually store a state of a bit! If we then put 32 copies of this circuit together, we can have a 32-bit storage register.
Again, it is useful to walk your way through the diagram to see where each state is one or zero at both the input and the output of EACH GATE.
Registers
OK, so what? Well, now that we have the ability to use gates to make a full adder, we have a way to add two numbers of multiple bits, handle the carry, and give a correct result. AND, now that we have a way to store a bit, we can gang a bunch of flip-flops together to make a way to store sequences of bits all at the same time! This is what is known as a register. That's just a fancy name for an internal memory location which can store bit patterns INSIDE the CPU so that it is very fast to access. We'll see how that is useful soon!
Stanley/Penguin — A Simple CPU
OK, now we have the basics of what internally makes up the CPU. Now, let's move on to defining our own simple CPU engine, in terms of its components and their operation. This will be a VERY simplified machine, to acquaint you with the way things work in our more sophisticated modern processors like the Intel and ARM processors that are in our computers, cell phones, tablets, and other devices. Another thing for which this machine is useful: giving you practice in thinking about the programming at the machine level. Machine-level programming is VERY specific and one must break the actions down much further than we are used to doing in high-level languages.
In honor of the Spring 2021 sections of what was then known as CMSI 284, this machine shall forever forward be known asStanley/Penguin.
History: the MWF section voted [NOT unanimously!] forStanley, and the T-Th section voted [closer but still not unanimously] forPenguin.
Since there were two names, I decided [in a unanimous vote of one] to call the machine and its languageStanley/Penguin.
— So let it be written; so let it be done!
Parts
The parts of our simple machine are:
- The Accumulator, abbreviated A which is a 32-bit register that stores our values; this is basically a 32-bit register, and every operation that the machine does will involve this part.
- The Instruction Pointer, abbreviated IP which is another 32-bit register, which is specially used to hold the address of the next instruction that is to be executed.
- 256 MiB words of memory, each of which is 32-bits wide, which is abbreviated
M; remember one
MiB
orMebibyte
is different than a Megabyte. A Megabyte is 1 million bytes but a Mebibyte is 1024 * 1024 or 220 bytes, which is actually 1,048,576 bytes. - The ports to which we can write information, and from which we can also read input; these are abbreviated P Note that ports are randomly selected from the memory space and are used for input and output as if from external devices like keyboards, screens, printers, etc. The selection of the port address is made so that it won't conflict with other memory locations which the program may need to use for storage.
Operation
Even though it is simple, our computer will still follow the Von Neumann Architecture operation of fetch, decode, and execute. At each "step", the computer reads the memory word whose address is in IP and then increments the value contained in IP. Then it decodes and executes the instruction which the fetched word represents.
This is how most computer CPU's [or cores] work, as you know from me beating that into your brains over several courses.
In this class, we're not too concerned with how steps are synchronized; we'll just say there's a clock.
Now, in order for meaningful work to be done, we need a way to decode the instructions once they have been obtained from memory. This mapping [AGAIN with that term!] is not entirely arbitrary in the real world, but for our purposes, it can be. Let's break it down.
To start with, we have 32 bits with which to work. Let's say we want to have 16 instructions, which will
be plenty for our rudimentary example purposes. We know from our previous discussions that 16 instructions
will require four bits of our 32-bit word to hold all the values, since the 16 values zero
through F will fit into four bits. That means we have 28 bits left over for things like
addresses and data values to associate with each instruction. The 4-bit operational values are called
operational codes or simply just opcodes. We'll define them as
follows:
| opcode | Action | Meaning |
|---|---|---|
| 0 | A := M[x] | Load the Accumulator from memory address [x] |
| 1 | M[x] := A | Store accumulator to memory |
| 2 | A :=P[x] | Read from a port into the accumulator |
| 3 | P[x] :=A | Write accumulator out to a port |
| 4 | A := A + M[x] | Add into accumulator |
| 5 | A := A - M[x] | Subtract from accumulator |
| 6 | A := A × M[x] | Multiply into accumulator |
| 7 | A := A ÷ M[x] | Divide accumulator |
| 8 | A := A mod M[x] | Modulo |
| 9 | A := A & M[x] | Bitwise AND |
| A | A := A | M[x] | Bitwise OR |
| B | A := A ^ M[x] | Bitwise XOR |
| C | IP := x | Set IP to jump to new address for next instruction |
| D | if A = 0 then IP := x | Jump if accumulator is zero |
| E | if A < 0 then IP := x | Jump if accumulator is less than zero |
| F | if A > 0 then IP := x | Jump if accumulator is greater than zero |
For those who may be familiar with modern processors, note a few [somewhat daunting] restrictions. First
there is only one Accumulator, and we can't easily break it into sections of smaller-sized bytes or word
values. Secondly there is no indirect addressing
in which we can use a memory location to point
to ANOTHER memory location into which to read/write data. Another thing that is missing is the
Instruction Register which is where the fetched instruction would be held so that it
can be decoded. There are others, as well. However, for the purposes of illustration and to get you
familiar with the way processors generally work, this one will suffice. Note that all arithmetic is
signed, modular, 32-bit operations.
Illustrating What Happens Inside
The order of operations of our processor is exactly as you would expect with the Von Neumann Architecture.
First the address that is pointed to by the IP is used to fetch the next instruction from memory. Then,
the instruction is decoded, meaning the first four bits are translated into their instruction,
and the last 28 bits are translated into the memory location for that instruction. For example, assume
that the instruction fetched is 0x4FFFFFFF which is the hex value for the binary code
0100 1111111111111111111111111111. The first four bits give us the opcode,
interpreted as A := A + M[x]. The value of x is, of course, the last 28 bits,
which in this case is 0xFFFFFFF or the value 268,435,45510. Since
this is the highest value we can have for our memory, that means Load the Acumulator with the
value stored at the highest address in memory
Thus:
- Fetch: load the value from address
xinto the instruction register for decoding - Decode: decode the 32-bits into the opcode and the address
- Execute: make it happen in the logic of the processor
Executing the Instruction
Here is a sample program [Thanks, Dr. Toal!] which when loaded into the memory of our simple computer
will output a listing of the powers of two, starting with 1 and continuing until it gets
just past 1,000,000. The output will be sent to port 100 [port 0x64]:
C0000003 [jump to address 0x0000003, start of program]
00000001 [load A with data value at address 0x0000001; 'start']
000F4240 [load A with data value at address 0x00F4240; 'limit']
00000001 [load A with start value at address 0x0000001]
30000064 [output A's value to port ix100]
40000001 [add value of address 0x0000001 to A]
10000001 [store value of a to address 0x0000001]
50000002 [subtract value of 'limit' from A]
E0000003 [if result is less than zero, jump to 0x0000003]
C0000009 [stop]
Of course, this is all theoretical at this point. There *IS* no physical machine like this, no ports, no actual memory, no processor, no IP or A or anything else. But, the concepts show you exactly the kind of thing that happens in your computer, even as you are reading this on your computer screen!
Writing Programs
OK, now we know how things will work, so now we can program our machine. But wait, hold up. Who the heck wants to program using binary or hex code?!? Nobody *I* know would write code that way UNLESS they have a specific need to handle computations at the lowest possible level. So, we need a language that makes more sense to humans so that we can do this task more easily. Enter the assembler!
The assembler acts as a translator that allows us to write our programs using mnemonics that are more intelligible to humans, then translate that code into the binary machine code that the computer will understand and use. We've already seen a low-level example, so let's take a look at the table again with the mnemonics included:
| opcode | Action | Mnemonic | Meaning |
|---|---|---|---|
| 0 | A := M[x] | LOAD | Load the Accumulator from memory address [x] |
| 1 | M[x] := A | STORE | Store accumulator to memory |
| 2 | A :=P[x] | READ | Read from a port into the accumulator |
| 3 | P[x] :=A | WRITE | Write accumulator out to a port |
| 4 | A := A + M[x] | ADD | Add into accumulator |
| 5 | A := A - M[x] | SUB | Subtract from accumulator |
| 6 | A := A × M[x] | MUL | Multiply into accumulator |
| 7 | A := A ÷ M[x] | DIV | Divide accumulator |
| 8 | A := A mod M[x] | MOD | Modulo |
| 9 | A := A & M[x] | AND | Bitwise AND |
| A | A := A | M[x] | OR | Bitwise OR |
| B | A := A ^ M[x] | XOR | Bitwise XOR |
| C | IP := x | JMP | Set IP to jump to new address for next instruction |
| D | if A = 0 then IP := x | JZ | Jump if accumulator is zero |
| E | if A < 0 then IP := x | JLZ | Jump if accumulator is less than zero |
| F | if A > 0 then IP := x | JGZ | Jump if accumulator is greater than zero |
Now that we have the mnemonics for the assembly language for this machine, we can write code which looks more like what we're used to seeing when we program in any other language! Here is the previous code with the machine language that was in the previous block along with its associated assembly language:
C0000003 JMP start ; begin by jumping over the data area
00000001 pow: 1 ; store the current power value here
000F4240 limit: 1000000 ; we'll be computing powers up to this amount
00000001 start: LOAD pow ; bring the value into accumulator to use
30000064 WRITE 100 ; output the current power
40000001 ADD pow ; adding to itself makes the next power!
10000001 STORE pow ; store it (for next time)
50000002 SUB limit ; we need to compare with limit, subtracting helps
E0000003 JLZ start ; if not yet past limit, keep going
C0000009 end: JMP end ; this "stops" the program!
Investigation: Write a program in our new assembler to write the first 10 Fibbonaci numbers to port 255.
Investigation: Write a program for this computer to output Hello, world to port 888, assuming a UTF-32 encoding.
Investigation: Write, in the language of your choice, an assembler for this computer. You will have to make a number of decisions regarding the user interface. Be creative.
Investigation: Write a program in our new
assembly language to check if the word RACECAR
is a palindrome.
Discussion: Suppose you were disassembling the word 100038A0
from our machine's instruction set. Is this an instruction to store the accumulator into memory address
0x00038A0, or is it a representation of the value 268449952? Or is it both?
Why is this question philosophically interesting?
Machine Language
It should be quite clear to you now that the machine language of our little processor is the patterns of ones and zeros that we create by assembling the mnemonic code we write in our assembler language. Thus, assembly language is NOT machine code! This is an important distinction which many programmers lose sight of – since we normally write programs in a high-level language like Python, we are a couple of levels above what is happening at the lower levels of the machine architecture [remember the layered block from week 2?]
This leads to another concept of which we should be aware. The ordering of the bytes in memory is important. Since we defined the 32-bit values of our machine language in a certain way, having the first four bits being the opcode, we need to make sure that the first four bits are REALLY the first four bits!
Wait…… WHAT?!
In the book Gulliver's Travels by
Jonathan Swift, there are two political factions who are divided over which end of an egg to crack. A
part of the population avowed that one should start with the big end [Big Endians
], and the other
group steadfastly maintained it should be the little end [Little Endians
]. This idea has been
adopted for computer purposes to label the two different ways that multiple bytes of data are stored.
This is important to us because virtually all modern processors and memories are able to use single bytes of information, but different architectures may store/retrieve them in different orders. Usually UNIX computers are big endian, while Windows boxes are little endian. So the way the bytes are stored in memory and handled by the processor matters when you need to insure that you are getting the byte you think you are getting.
For example, consider our 32-bit word
, which is four bytes:
| Byte 3 | Byte 2 | Byte 1 | Byte 0 |
|---|
On a little endian machine, the four bytes are arranged like so:
Base Address + 0 → Byte 0
Base Address + 1 → Byte 1
Base Address + 2 → Byte 2
Base Address + 3 → Byte 3
…which means that the LEAST significant byte is stored at the base address as you can see. However, on a big endian machine, they are arranged thus:
Base Address + 0 → Byte 3
Base Address + 1 → Byte 2
Base Address + 2 → Byte 1
Base Address + 3 → Byte 0
There are advantages and disadvantages to each method. Big endian seems more natural to most people, so it is easier to read through hex data. Having the high-order byte come first makes it easier to figure out integer sign information. Big endian is faster in string operations since the characters are stored in the correct order [for L-to-R languages]. Most bit-mapped graphics have the MSB on the left so the graphics architecture can handle the bytes easily. Decoding of compressed data using Huffman or LZW is easier when the byte order is big endian because of the hashing of the bytes/words. Diagramming the way the value looks in memory is easier too [for the western mind] because it goes left-to-right like we are used to seeing.
On the other hand, the little endian schemes allow data to be written to memory on non-word address
boundaries
. For exampe, if a word is 2 or 4 bytes, it must always begin on an even-number byte
address on a little endian machine, which can waste memory space.
Computer networks, by the way, are big endian. This means that when little endian computers are going to send integer values [or any values larger than a single byte] they must convert their byte order to network byte order. See this page for more details on what is often called the NUXI problem.
This is also important for file I/O. Any program that reads or writes data to a file must be aware of the byte ordering on both the machine it is written from and the machine it will be read on.
CISC and RISC
There are two other flavors
of processor architecture which must be mentioned. Most of what we
have been dealing with up to this point is known as the Complex Instruction Set Computer
or CISC
machine. The other version of this is called Reduced Instruction Set Computer
or RISC
machines.
Complex instruction set designs were motivated by the high cost of memory. Having more complexity packed into each instruction meant that programs could be smaller, thus occupying less storage. CISC architecture machines use variable-length instructions, keeping the simple instructions short, while also allowing for longer, mor complicated instructions. Additionally, CISC architectures include a large number of instructions that directly access memory. CISC machines provide a dense, powerful, variable-length set of instructions, which results in a varying number of clock cycles per instruction. Some complex instructions, particularly those instructions that access memory, require hundreds of cycles. In certain circulstances, computer designers have found it necessary to slow down the system clock [meaning they make the interval between clock ticks larger] to allow sufficient time for instructions to complete. This all adds up to longer execution time.
RISC computers are so named because the originally offered a smaller instruction set as compared to CISC
machines. As RISC machines were being developed, however, the term reduced
became somewhat of a
misnomer, and it is even more so now. The original idea was to provide a set of minimal instructions
that could carry out all essential operations. Only explicit load and store
instructions were permitted to access memory directly. Further, most RISC instructions execute in a
single clock cycle. This was accomplished by replacing microcode control with hardwired
control, which is faster at executing instructions. [Remember the old adage that anything you can do
in software you can do faster in hardware
to supply the rationale for this fact.]
As an example, consider the following computation. Suppose we want to multiply the values 23 × 17. The CISC code would look like:
mov ax, 23
mov bx, 17
mul bx, ax
A minimal RISC computer has no mul
instruction! The same operation would appear this
way on a RISC machine:
mov ax, 0
mov bx, 17
mov cx, 23
begin: add ax, bx
loop begin
Note that the last RISC instruction cause the loop to execute cx
times, since cx is used as a
loop invariant in RISC machines. Note also that the CISC instructions, while shorter, will require
more clock cycles than tne RISC version.
Another feature of RISC machines is the larger number of registers. A register is a special type of memory that is built right onto the CPU chip, so it is VERY fast to access. The more registers you have on the chip, the faster your programs can run.
Why do we care about RISC computers? Well, in two words, ARM Processor. This is the processor that is used in most mobile devices such as smart phones, laptops, tablets, music players, and other embedded systems.
In-class Exercise #6
From the four investigations above, pick one to do as an exercise in class.
If you finish before class is over, pick another one and work on that as well.
Be sure to check your work into your GitHub repo!
Homework Assignment #4
I know this isn't due until next week, but i wanted to give you a heads-up on the homework assignments that you will be doing this semester. They are all available from the syllabus page, but just to make sure …
Week Six Wrap-up
That's probably enough for the this week. Be sure to check out the links to the related materials that are listed on the class links page.