CMSI 284: Welcome to Week 03
This Week's Agenda
For this week, here's the plan, Fran…
- Announcements
- Information Representation
- Symbols and Alphabets
- Encoding Schemes
- Bit String Encoding
- Functions
- Function Machines
- Programming as Machine Creation
- Encoding Schemes – numeric, fixed-size, floating point
- Thursday/Friday: In-class Exercise:
Information Representation
Once we understand some of the internal parts of a computer system and see how those parts are organized,
we need to start understanding how different data are handled by the machine. The first thing to note
is that since everything in the machine is binary [either on or off] we need to store ALL values using
some sort of binary representation. That means we don't just jam the number 32767
in its base-10
form into some register in the CPU – instead, we need to translate it into its equivalent binary
representation.
This fact also means we need to explore just what the symbols and alphabets of human-usable information look like. Some examples of these symbols follow [thanks Dr. Toal!]:
- 91442.3e-4
- Stay behind the yellow line!
- /Pecs/Los Angeles/Berlin/Madrid//1 2/3 0/2 2/2 0/3 2///
- (* (+ 4 3) (-9 7))
- int average(int x, int y) {return (x + y) / 2;}
Lisichka 13 - {"type": "dog", "id": "30024", "name": "Lisichka", "age": 13}
- ∀α β. α⊥β ⇔ (α•β = 0)
- 1. f3 e5 2. g4 ♛h4++
- 1,$ s/this is a test/this is a string/g
- wq!
Symbols and Alphabets
The symbols that make up pieces of data are chosen from some finite alphabet, such as {0,1,2,3,4,5,6,7,8,9} for the language of natural numbers, or {0,1,2,3,4,5,6,7,8,9,e,E,+,-,.} for the language of floating-point numbers. In reality, the alphabet you choose is irrelevant because it is always possible to recode any alphabet into a two-symbol alphabet.
For example, let's say you have an alphabet {a,b,c,d,e,f,g}. You can recode this into the alphabet {0,1} as follows:
| a → 000 |
| b → 001 |
| c → 010 |
| d → 011 |
| e → 100 |
| f → 101 |
| g → 110 |
Then the word cab becomes 010 000 001 in the new alphabet! Actually, though, it turns into 010000001 – the spaces were put in for clarity. The word face turns into 101 000 010 100; the word bagged becomes 001 000 110 110 100 011.
Discussion Question: Alert reader Chester T. Fahrquar of Teaneck, New Jersey
writes in and asks:
Yeah, but why can't we just do a → 0 , b → 1,
c → 10, d → 11, e → 010… wouldn't that work just as well?
How would you answer Chester's question?
In fact, ANY information [whether it be numbers, characters, programming instructions, pictures, or even complex data of any kind] can be encoded in strings from {0,1}, which we call bit strings, since they are bits that are strung together.
Discussion Question: How might you encode pictures and audio and video with bits?
To make it easier to visualize values and collections of bits, we group them together into sets of eight, called bytes [or sometimes called octets which is actually more correct but less common].
Bit strings can get very long as you might imagine, since EVERYTHING is encoded into strings of them. For example consider a small picture of 100 x 100 pixels. On a color screen each pixel's information might be stored in 24 bits, eight bits for the strength of each color, Red, Green, and Blue. For that picture there would be 100 x 100 = 10,000 pixels, at 24 bits each, would be 24,000 bits!
Even shorter strings of bits can become hard for humans to deal with, so we often compress them by naming
chunks of 4 bits at a time. This representation is known as hexadecimal because it is
using base-16 instead of base-2 or base-10. You will learn more about hex
soon.
For now, the encoding is as follows:
| 0000 → 0 |
| 0001 → 1 |
| 0010 → 2 |
| 0011 → 3 |
| ... |
| 1000 → 8 |
| 1001 → 9 |
| 1010 → A |
| 1011 → B |
| 1100 → C |
| 1101 → D |
| 1110 → E |
| 1111 → F |
That way, instead of writing
10000111110001000100111110101001
you can just write
87C44FA9
Click for Some History
Bit String Encoding
Since everything can be encoded into bit strings, decoding a bit string into the item it encodes depends
on how it is interpreted [or in the vernacular of computer science, decoded
]. For example, the
same bit string 1101010010110010 [or 0xD4B2 in hex; note the leading 0x
]
has the following different meanings based on the encoding used.
[You don't have to know what these interpreations are for now, you just need to appreciate that
the different interpretations exist]:
| Interpretation | Meaning |
|---|---|
| Unsigned Short Integer | 54450 |
| Signed Short Integer | -11086 |
| UTF-16 String | The character HANGUL SYLLABLE PHIEUPH WE SSANGKIYEOK: 풲 |
| UTF-8 String | The character ARMENIAN CAPITAL LETTER BEN: Բ |
| ISO 8859-1 String | The two-character string LATIN CAPITAL LETTER O WITH CIRCUMFLEX followed by the SUPERSCRIPT TWO: Ô² |
| IA-32 Machine Instruction | An instruction that will divide the value in the AL register by 178, placing the quotient in the AH register and leaving the remainder in AL |
Functions
Information Processing is the transformation of one piece of data into another; the mathematical abstraction of this transformation is called a function. You probably already have a sense of functions. Consider:
double, which takes a number and returns twice that numberplus, which takes a pair of numbers and returns their sumnextMove, which takes a state of a game and returns the next (best?) move that should be madeupperCase, which takes a piece of text and returns a string like it but with all letters capitalizedsorted, which takes a list of things and returns a new list containing the same values in sorted ordereven, which takes a number and returns true or false depending on whether the number is eventint, which takes an image, a color value, and a number, and tints the image with the given color by the given amounttwice, which takes a function and a value and applies the function to the result of applying the function to the value
An infinite number of functions exist. Note to mathematicians: there exists an uncountably infinite number of possible functions.
Functions are applied to arguments to produce their results. For example:
double(3.5) ⇒ 7plus(4, -3) ⇒ 1upperCase("Please don't shout!") ⇒ "PLEASE DON'T SHOUT!"sorted([4, 7, 1]) ⇒ [1, 4, 7]even(797) ⇒ falsetwice(double, 5) ⇒ double(double(5)) ⇒ double(10) ⇒ 20
To define a function, we specify the rule that transforms the arguments into the result, often making use of existing functions. One way to do this is pictorially. Here we define a function to tell whether a number is odd:
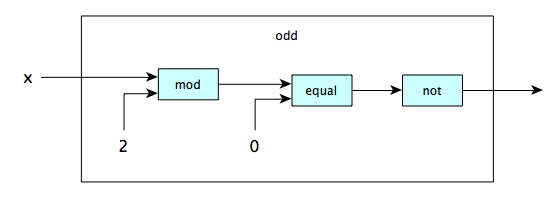
In this function machine
there is a single input and a single output. The input is passed to an
internal function called mod which produces the remainder, as you know. The value
produced is passed to another internal function called equal which determines if it
is equal to zero. THAT result is passed to a third internal function called not which just
takes whatever is true and makes it false and vice-versa. The ultimate result, of course, is if the
value of X at the input is odd the value at the output will be true.
There are a couple of interesting things to note about this function. First, it follows the same process
as all computation, of input → process → output. Second,
it shows that there are sub-functions
within the odd function which assist in the
processing. Third, you can see similar modeling in Object-Oriented program languages like Java, C++, and
C# when you encounter expressions like:
return this.removeLeadingZeros( this.subtract( this.divide( bint ).multiply( bint ) ) );
Here is a function that computes the balance of an account with starting principal value p,
an annual interest rate r, the number of compounding periods per year n, and the
number of years t:
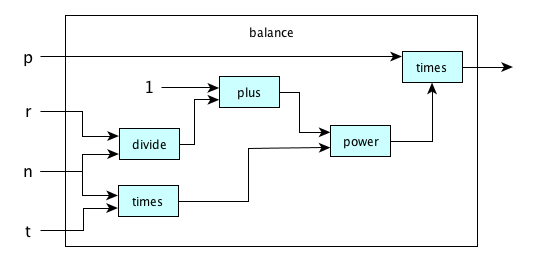
This one actually is the implementation of the compound interest formula from finance which looks like:
p x (1 + (r/n))nt ⇒ output
…which is normally written when programming it as:
output = p * ((1 + (r/n))**(n*t))
Function Machines
We can build machines to do ALL KINDS OF THINGS by executing functions — to capitalize text, to find
words in text, to compute interest payments, to add numbers, to send texts to us when something happens,
and on and on. But functions can be written as text, so maybe we can build a machine [let's call it
U], such that when you give it a function f (as text)
and some data x, then U will produce
f(x)? That is:
U(f,x) = f(x)
As it turns out, for a certain class of functions, you can construct such a machine. You might take that for granted today, but it was not obvious until the 20th century! [As far as anyone knows, that is.] This profound result is due to Alan Turing, and it pretty much changed the world. This U is called the Universal Turing Machine in his honor. Today we build variations of the original U. We call them computers.
Programming as Machine Creation
Thanks to Turing's insights, it is possible to make machines that can compute just about anything. All we need is a way to describe a computation and then give that description together with some input data and tell your universal machine to simulate the computation.
The way you describe computations depends on your programming language. One very cool language is called Python. You can write and run Python many places online [for example here], or go to python.org and get yourself a Python interpreter for your own machine [unless you have one already, which you do if you are on a mac, but an old version].
Here is a program in Python that you can enter and run. It defines the two functions we've been looking at earlier, and calls them with various arguments.
def odd(x):
return x % 2 != 0
def balance(p, n, r, t):
return p * (1 + r/n) ** (n * t)
print(odd(-35))
print(odd(3278947239863000))
print(balance(1000, 12, 0.03, 5))
Encoding Schemes
Numbers and Numerals
A number
is just an abstraction of quantity. Humans started with
counting numbers like one, two, three, four and so on. Zero came later. Then someone realized that
subtracting six from two could be useful and so invented negative numbers. Then integer division led to
the creation of rational numbers, and other work resulted in irrational numbers, real numbers,
transfinite numbers, imaginary numbers, complex numbers and so on.
In our modern system, a number [count] is represented by a numeral
which is just an arbitrary, yet
generally accepted, symbol that represents that quantity. For example, the
number 7
represents a count of seven things. We could use the symbol
⩘
instead, and if someone had defined that aeons ago so that we all
understood and accepted that symbol to mean a group of seven items, so it would be.
Egyptian Numerals
Egyptians wrote numerals in hieroglyphs for thousands of years; here are the important symbols and their numeric values:
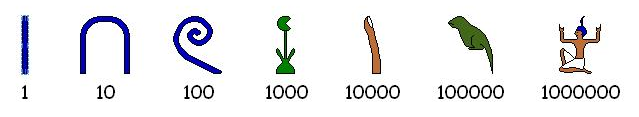
Notice that these numerals could be written from right-to-left or left-to-right or vertically or a combination of vertical and horizontal. Here is one way to represent twenty-one thousand two hundred thirty-seven:
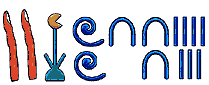
We don't use these numerals in computer systems today, but history is important, so please read more about these numerals at Wikipedia or elsewhere.
Exercise: Write out the number 5,994,998,999 using heiroglyphics. (Just kidding.)
Roman Numerals
Well, these aren't much use in modern computers, either. Enough said. Besides, they're really hard to understand, and they don't have a zero, or wait...maybe they do?
Roman Numerals did have a sort of primitive positional notaion
. If you know the symbols you can
interpret values by knowing that a symbol of lesser value that appearts before a symbol of greater
value is subtracted, and one that appears after is added. For example:
the value V
stands for the value 5
the value I
stands for the value 1
the value IV
then is 5 minus 1 or 4
the value VI
then is 5 plus 1 or 6
Here is a list of all the values and their related equivalents:
| I → 1 |
| V → 5 |
| X → 10 |
| L → 50 |
| C → 100 |
| D → 500 |
| M → 1000 |
As an exercise, see if you can express the current calendar year, 2021, in Roman Numberals.
Positional Numeral Systems
A Positional Numeral System
has an ordered set of digits
that includes 0 as its first member. The number of digits in the set is called the base. By far the most common of these is the Hindu-Arabic Numeral System, or Arabic Numeral System, which has a base of 10, and whose glyphs are these:
0 1 2 3 4 5 6 7 8 9
There are other positional systems, too:
- Devanagari (base 10)
- Mongolian (base 10)
- Kannada (base 10)
- Tamil (base 10):
- Maya (base 20)
- Kaktovik Iñupiaq (base 20)
In computing, though, the Hindu-Arabic numerals dominate. We can extend this system to bases other than 10 by adding or removing glyphs. Bases up to 36 are traditionally handled by adding the Latin letters A-Z. The most common systems in computing are:
- Decimal: digit set =
{0,1,2,3,4,5,6,7,8,9}, base = 10. - Octal: digit set =
{0,1,2,3,4,5,6,7}, base = 8. - Hexadecimal: digit set =
{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, base = 16. - Binary: digit set =
{0,1}, base = 2.
You generate positional numerals starting at 0 by a really easy algorithm you already know.
| Decimal | Octal | Hex | Binary |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 10 | 8 | 1000 |
| 9 | 11 | 9 | 1001 |
| 10 | 12 | A | 1010 |
| 11 | 13 | B | 1011 |
| 12 | 14 | C | 1100 |
| 13 | 15 | D | 1101 |
| 14 | 16 | E | 1110 |
| 15 | 17 | F | 1111 |
| 16 | 20 | 10 | 10000 |
| 17 | 21 | 11 | 10001 |
| 18 | 22 | 12 | 10010 |
| 19 | 23 | 13 | 10011 |
| 20 | 24 | 14 | 10100 |
| 21 | 25 | 15 | 10101 |
| 22 | 26 | 16 | 10110 |
| 23 | 27 | 17 | 10111 |
| 24 | 30 | 18 | 11000 |
| 25 | 31 | 19 | 11001 |
| 26 | 32 | 1A | 11010 |
| 27 | 33 | 1B | 11011 |
| 28 | 34 | 1C | 11100 |
| 29 | 35 | 1D | 11101 |
| 30 | 36 | 1E | 11110 |
| 31 | 37 | 1F | 11111 |
| 32 | 40 | 20 | 100000 |
| 33 | 41 | 21 | 100001 |
| ... | ... | ... | ... |
Third Graders, Binary Numbers, and the Socratic Method
For some inspiration, read about a third grade class's adventures in learning about and using binary numerals.
Conversion Between Number Bases
OK, now we know more about number systesms and positional notation, and we've analyzed how these systems
work to represent numbers. The all use the same idea of place value
with each successive place to
the left being one exponent value higher than the one before it.
So now, let's see how to convert Hex to and from Binary. But wait, this is trivial! Each group of four bits maps exactly to one hex digit! MEMORIZE THE MAPPING SO YOU CAN DO THE CONVERSION BY SIGHT. [Or, memorize the easy way to reproduce the first 16 rows of the table above.] Examples:
48C = 0100 1000 1100
CAFE54 = 1100 1010 1111 1110 0101 0100
Hex to Decimal: All Arabic numeral systems use place values which you should already be aware of. Examples:
E2A = 14(162) + 2(161) + 10(160)
= 14(256) + 2(16) + 10
= 3626
For numbers involving only two hex-digits you can do this in your head if you have memorized your
multiples of 16: 0→0, 1→16, 2→32, 3→48, 4→64, 5→80, 6→96, 7→112,
… F→224, F→240. This gives you the contribution of the first hex digit, so just add
in
the second.
Decimal to Hex: Keep on dividing by 16, working your way backwards. Example:
3653
/ \
228 5
/ \
14 4
/ \
0 14
==> E45
Binary to Decimal: Read left-to-right, doubling as you go and adding one where necessary. Example:
10110110
Say 1, 2, 5, 11, 22, 45, 91, 182.
Very easy! Of course, once you're a pro you might just say:
176 + 6 = 182
because you immediately see the 8 bits as a 1011 and a 0110, i.e., an 11 and a 6, and
16 × 11 is 176, etc.
This method is, in some circles, known as Dorin's Way.
What about conversion between arbitrary bases? Well, it's pretty cool to know how to do some generic conversions, but our focus today is stricly on binary, hex, and decimal. Leave converting from decimal to base 23 for a party sometime.
Addition
You learned the addition method a long time ago for decimal numerals; the same idea applies to all other number bases.
Examples in Binary
11010 101111 001 01
01101 111101 111 00
100111 1101100 1000 01
Examples in Hex
D371 9 37EE 89CA
26A2 9 F0 CC18
FA13 12 38DE 155E2
Subtraction, Multiplication, and Division
You probably learned algorithms for these operations, long ago; the good news is that it doesn't matter what number base you use — they are base-independent. Try some of these out in binary: you'll find they're quite simple, though they might take longer since there are so many bits, even for small quantities.
Encoding Integers in Fixed Length Bit Strings
Computers have storage locations with a fixed number of bits. The bits are numbered starting at the right-most bit, which is bit zero, also known as the least significant bit or LSB The other end, of course is the most significant bit or MSB. Examples:
| 3 | 2 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 15 | 14 | 13 | 12 | 11 | 10 | 09 | 08 | 07 | 06 | 05 | 04 | 03 | 02 | 01 | 00 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
Storage locations come in many sizes. Usually we write the values in a storage location out in hex; the
contents of our above examples are C, A7, and 3F25, respectively.
An n-bit storage location can store 2^n distinct bit strings so it can encode
(unsigned
) integers from 0 through 2^n-1. If we want to include some
negative numbers (signed
) we have several encoding options, but by far the most common is called the
Two's Complement Representation, which allocates the bit strings to the numbers
-2^{n-1} through 2^{n-1}-1. Note that a given bit string can be interpreted as
either an unsigned number or a signed one.
Here's how things look in a four-bit storage location, with signed values using the two's complement representation:
| Binary | Hex | Unsigned Decimal | Signed Decimal |
|---|---|---|---|
| 0000 | 0 | 0 | 0 |
| 0001 | 1 | 1 | 1 |
| 0010 | 2 | 2 | 2 |
| 0011 | 3 | 3 | 3 |
| 0100 | 4 | 4 | 4 |
| 0101 | 5 | 5 | 5 |
| 0110 | 6 | 6 | 6 |
| 0111 | 7 | 7 | 7 |
| 1000 | 8 | 8 | -8 |
| 1001 | 9 | 9 | -7 |
| 1010 | A | 10 | -6 |
| 1011 | B | 11 | -5 |
| 1100 | C | 12 | -4 |
| 1101 | D | 13 | -3 |
| 1110 | E | 14 | -2 |
| 1111 | F | 15 | -1 |
For 32-bit locations there are 4294967296 possible bit strings; here are some of them:
| Binary | Hex | Unsigned Decimal | Signed Decimal |
|---|---|---|---|
| 00000000000000000000000000000000 | 00000000 | 0 | 0 |
| 00000000000000000000000000000001 | 00000001 | 1 | 1 |
| ... | ... | ... | ... |
| 01101000101011111110000100001101 | 68AFE10D | 1756356877 | 1756356877 |
| ... | ... | ... | ... |
| 01111111111111111111111111111110 | 7FFFFFFE | 2147483646 | 2147483646 |
| 01111111111111111111111111111111 | 7FFFFFFF | 2147483647 | 2147483647 |
| 10000000000000000000000000000000 | 80000000 | 2147483648 | -2147483648 |
| 10000000000000000000000000000001 | 80000001 | 2147483649 | -2147483647 |
| ... | ... | ... | ... |
| 10010111010100000001111011110011 | 97501EF3 | 2538610419 | -1756356877 |
| ... | ... | ... | ... |
| 11111111111111111111111111111110 | FFFFFFFE | 4294967294 | -2 |
| 11111111111111111111111111111111 | FFFFFFFF | 4294967295 | -1 |
Here are some values that can represented in locations of different sizes:
| Bits | Unsigned Range | Signed Range |
|---|---|---|
| 8 | 00…FF 0…255 | 80…7F -128 …127 |
| 16 | 0000…FFFF 0 …65,535 | 8000…7FFF -32,768 …32,767 |
| 24 | 000000…FFFFFF 0…16,777,215 | 800000…7FFFFF -8,388,608…8,388,607 |
| 32 | 00000000…FFFFFFFF 0…4,294,967,295 | 80000000…7FFFFFFF -2,147,483,648…2,147,483,647 |
| 64 | 0000000000000000…FFFFFFFFFFFFFFFF 0…18,446,744,073,709,551,615 | 8000000000000000…7FFFFFFFFFFFFFFF -9,223,372,036,854,775,808… …9,223,372,036,854,775,807 |
Fixed-Length Integer Addition
With adding numbers using fixed length storage locations, the number of bits of the result may not always fit into the space provided by the fixed number of bits. This is called overflow.
For example: given an 8-bit location, and adding the unsigned numbers C5 + EE. The result
value should be 1B3, but that won't fit because it requires NINE BITS!
Another way to check this is to conceptually consider it. In this problem, the decimal values involved
are 197 + 238 = 435. Since the largest unsigned value that will fit into an 8-bit space is
when all eight of the bits are 1, the maximum decimal value that fits is 255.
The resulting addition is outside that range of 0..255, so it overflows.
Saturated vs. Modular Addition
There are two main approaches to dealing the problem of a sum not being able to fit. We could:
- Clamp the sum at the maximum representable value. This is called
saturated arithmetic. In the previous example the sum would be
FF[or 255 decimal] - Ignore the carry, making our example's result as
B3. This is called modular [or wraparound] arithmetic
What about signed numbers? For example: Try 6C + 53. You get 6C + 53 =
BF. Well, you didn't carry anything out when you added, but there is still a problem. Given the
convention that the highest-order bit being set
indicating a negative number, you have added two
positive values and ended up with a negative result! So, even though the answer still fits in 8 bits,
this too, is overflow. Again we could:
- Clamp the sum at the maximum representable value [which in the above example is 7F]
- Leave the result as BF
Almost all computers do modular arithmetic. Some do modular and saturated arithmetic [e.g. In the Intel
x86 family modular addition is done with the add or padd instructions, and
saturated addition is done with padds or paddus instructions.
Overflow Detection
You have to know how to detect overflow. For unsigned numbers this occurs precisely when you carry out of the highest order bit. For signed numbers this occurs precisely when you've added two positive numbers and gotten a negative result, or added two negative numbers and gotten a positive result.
Examples of signed modular addition in 8-bit storage locations:
1 1 1 1 11 11 <— carry row
2C 78 42 E0 87 FF
38 6A FC 75 DA C1
64 E2 3E 55 61 C0
cry:no cry:no cry:yes cry:yes cry:yes cry:yes
ovf:no ovf:yes ovf:no ovf:no ovf:yes ovf:no
Subtraction for Fixed-Length Integers
Because of the cool way the two's complement representation works, you can subtract a-b by
computing a+(-b). So just find the additive inverse of b and
add it to a. By the way, someone with a really sick sense of humor called the additive
inverse the two's complement and the name stuck. Finding the additive inverse is easy:
just invert every bit and add 1 to the result!
But hold on there Little Buckaroo! Before you start doing this, MAKE SURE YOU UNDERSTAND WHY THIS TECHNIQUE IS CORRECT!
Example in 8 bits: 44 decimal is 2C in hex or
00101100 in binary. So -44 decimal is found like this
00101100 =====invert bits=====> 11010011
add 1=====> 1
--------
11010100 ==> D4.
So this says that 2C and D4 are inverses. To do a sanity check, add the two
together and make sure you get a result of zero.
Check: 2C + D4 = 00.
OK, now we have what we need to do subtraction using addition. Let's take the problem 123 - 45
which in hex is 7B - 2D and in binary is 01111011 - 00101101. First find the
complement of 00101101 which is 11010011, then add that to 01111011:
01111011
+ 11010011
101001110
↑ 4 E ←—— converting: 64 + 14 is 78 [correct answer]
|
+--------- note overflow, which we ignore [modular addition]
A subtraction example in 8 bits:
[two's complement of -83]
↓↓
E2-83 = E2+(-83) = E2 + 7D = 5F
or in decimal: -30 + 125 = 95
By the way, if you start thinking in hex
, you can do this stuff much faster. We'll see better
techniques in class.
Prefix Multipliers for Sizes in Bytes
When numbers get really large you can use some special values:
| Powers of Tens | Powers of Twos | ||||||
|---|---|---|---|---|---|---|---|
| k | kilo | 103 | Thousand | Ki | kibi | 2 10 | 1,024 |
| M | mega | 106 | Million | Mi | mebi | 2 20 | 1,048,576 |
| G | giga | 109 | Billion | Gi | gibi | 2 30 | 1,073,741,824 |
| T | tera | 1012 | Trillion | Ti | tebi | 2 40 | 1,099,511,627,776 |
| P | peta | 1015 | Quadrillion | Pi | pebi | 2 50 | 1,125,899,906,842,624 |
| E | exa | 1018 | Quintillion | Ei | exbi | 2 60 | 1,152,921,504,606,846,976 |
| Z | zetta | 1021 | Sextillion | Zi | zebi | 2 70 | 1,180,591,620,717,411,303,424 |
| Y | yotta | 1024 | Septillion | Yi | yobi | 2 80 | 1,208,925,819,614,629,174,706,176 |
| X | xona | 1027 | Octillion | Xi | xobi | 2 90 | 1,237,940,039,285,380,274,899,124,224 |
| W | weka | 1030 | Nonillion | Wi | webi | 2100 | 1,267,650,600,228,229,401,496,703,205,376 |
| V | vunda | 1033 | Decillion | Vi | vubi | 2110 | 1,298,074,214,633,706,907,132,624,082,305,024 |
| U | uda | 1036 | Undecillion | Ui | udbi | 2120 | 1,329,227,995,784,915,872,903,807,060,280,344,576 |
(Everything up to yotta is part of the official SI system of units. The xona, weka, etc. prefixes are
under consideration; alternatives for 10^{27} and 10^{30} are nona and dogga
… because it's fun to say doggabyte.
) Possibly even better: There is an
online
petition you can sign to get the SI to make hella
the official prefix for 1027.
Examples:
4 Ki = 22210 = 212 = 4096
64 Ki = 26210 = 216 = 65536
256 Ki = 28210 = 218 = 262144
16 Mi = 24220 = 224 = 16777216
4 Gi = 22230 = 232 = 4294967296
32 Ti = 25240 = 245 = 35184372088832
2 Pi = 21250 = 251 = 2251799813685248
1 EiB is 1024 PiB.
Exercise: Find out how much printed information exists in the world; express the value in exabytes.
Exercise: How many exabytes worth of information has Facebook amassed?
Real Numbers
A real number is, well, I leave it to you to look up its formal mathematical definition because it isn't really trivial. But you should have some idea. The important thing here is: how can we represent them in fixed-length storage locations? We could use integer pairs for numbers we know to be rational, or take a long string and assume the decimal point is always in a certain place (called a fixed-point representation), or use a floating-point representation.
Encoding Floating Point Numbers in Fixed Length Bit Strings
Most modern general purpose computers use an encoding scheme for floating point values called IEEE 754. There are (at least) two representations. One uses 32-bits and the other uses 64-bits.
IEEE 754 Single-Precision (32 bits) Representation
The thirty-two bits are broken into three sections, the sign (s), the fraction (f), and the exponent (e).
| 31 | 30 | 23 | 22 | 0 |
| s | e | f | ||
Taking s, f, and e as unsigned values, the value of the number, in decimal, is:
| e | f | s | value |
|---|---|---|---|
| 1..254 | anything | 0 | (1 + f × 2-23) × 2e-127 |
| 1 | -(1 + f × 2-23) × 2e-127 | ||
| 0 | 0 | 0 | +0 |
| 1 | -0 | ||
| not 0 | 0 | (f × 2-23) × 2-126 | |
| 1 | -(f × 2-23) × 2-126 | ||
| 255 | 0 | 0 | +infinity |
| 1 | -infinity | ||
| 1...222-1 | anything | Signaling NaN | |
| 222...223-1 | Quiet NaN |
When we assemble the number, we start with 1.0 and add the fractional part as a decimal.
Then we use the exponent to move the decimal point to its appropriate spot. The sign bit is obvious.
So as an example: What does C28A8000 represent? In binary, it is
11000010100010101000000000000000, so:
s e f
1 10000101 00010101000000000000000
So, s = 1, e = 133, f = 00010101 [this is the fraction part
the LSB is at the left end]
Remember from the table above, the value will be (1 + f + 2-23) × 2e-127.
So, s = 1 means a negative number, e = 133 means our exponent will be
133 - 127 = 6 and f will be the MSB's of the fractional part. Our value is then
-(1.00010101)2 × 26 = -(1000101.01)2 which is clearly
-69.25 in decimal.
IEEE 754 Double-Precision (64 bits) Representation
The sixty-four bits are broken into three sections, the sign (s), the fraction (f), and the exponent (e) just like before, only with a LOT more digits. Twice as many, to be exact, since this is a 64-bit space and the other was a 32-bit space. [Duh!]
| 63 | 62 | 52 | 51 | 0 |
| s | e | f | ||
Taking s, f, and e as unsigned values, the value of the number, in decimal, is:
| e | f | s | value |
|---|---|---|---|
| 1..2046 | anything | 0 | (1 + f × 2-52) × 2e-1023 |
| 1 | -(1 + f × 2-52) × 2e-1023 | ||
| 0 | 0 | 0 | +0 |
| 1 | -0 | ||
| not 0 | 0 | (f × 2-52) × 2-1022 | |
| 1 | -(f × 2-52) × 2-1022 | ||
| 2047 | 0 | 0 | +infinity |
| 1 | -infinity | ||
| 1...251-1 | anything | Signaling NaN | |
| 251...252-1 | Quiet NaN |
Special Floating Point Values
NaN means not a number.
Quiet NaNs (QNaNs) propagate happily through these
computations. Signaling NaNs (SNaNs) can be used to signal serious problems. You can use them to
indicate uninitialized variables, for example.
- Overflowing addition, subtraction, multiplication gives the expected infinity
- Adding two positive infinities gives positive infinity
- Adding two negative infinities gives negative infinity
- But infinity minus infinity = NaN
- A finite value divided by an infinity = 0
- Any nonzero value divided by 0 = infinity
- But 0 / 0 = NaN
- infinity × 0 = NaN
- infinity × infinity = infinity
- infinity / infinity = NaN
- Any arithmetic operation on a NaN results in NaN
- A NaN never compares equal to anything, not even another NaN
More Information
Here's Tom Scott explaining floating point:
If you would like to see a more extensive summary of IEEE 754, see Steve Hollasch's. It is quite good. Oh, and you should read Goldberg's classic paper.
If you need to see online IEEE 754 converters, you can use mine (which is pretty good), or the one at City University of New York, which is awesome.
In-class Exercise #3
Learning outcomes: The student will learn more about 1) the way values are encoded in
real life situations; 2) that there is such a thing as Morse Code; and 3) the NATO phonetic alphabet
in case they want to use the real
words for things like NO, I mean S as in
Sam…
Your task this week is to work through the following encodings and write a short program for each one. Feel free to use any language you are familiar with, whether it be Python, Java, JavaScript, TypeScript, or anything else you want. Here are the problems:
- Write a program which takes in a word or phrase and produces a listing to the
terminal window which uses the standard NATO phonetic alphabet words for each letter. For example,
entering the word "hello" will produce the listing:
....and the phrase "blah blah" will produce:HOTEL ECHO LIMA LIMA OSCAR
There is no distinction required for upper or lower case letters, so you may treat them however you want. For a complete listing of the NATO alphabet, see the web page at this link.bravo lima alpha hotel bravo lima alpha hotel
[[Whiskey Tango Foxtrot, Viper command?]] - Do the same thing as in the previous problem, but produce the listing in the
Morse code rather than the NATO code. Use whatever characters you wish for the dots and the dashes
as long as the program specifies what you are using so the user can tell one from the other. For
example, you might want to use the period for the dot and the underscore for the dash, or the star
for the dot and the tilde for the dash. For example, the international distress code of
SOS
would be:
A listing of the Morse code is on the same page as the wikipedia link above.*** ~~~ *** - From "Python for Everyone" by Cay Horstmann and Rance D Necaise,
ISBN 978-1-118-62613-9
Business P2.36: [note: also a homework problem for CMSI 185] An online bank wants you to create a program that shows prospective customers how their deposits will grow. Your program should read the initial balance and the annual interest rate, either from the command line or from prompted user input. Interest is compounded monthly which will simplify the equation. Write a program to print out the balances after the first three months. Use the equation that is given above in the function description area of the page as a start. Here is a sample run:Initial balance: 1000 Annual interest rate in percent: 6.0 After first month: 1005.00 After second month: 1010.02 After third month: 1015.08
For a sanity check, here is a website that will do the calculation for you and print out the values in a table.
Homework Assignment #3
I know this isn't due until next week, but i wanted to give you another heads-up on homework assignments you will be doing this semester. They are all available from the syllabus page, but just to make sure I'm giving you a reminder…
Week three Wrap-up
That's probably enough for the this week. Be sure to check out the links to the related materials that are listed on the class links page.